Logistic 回归虽然名字里带 “回归”，但它实际上是一种二分类方法，即 LR 分类器（Logistic Regression Classifier），其数学模型是一个 sigmoid 函数，因图像像 S，又经常称之为 S 形曲线，sigmoid 本身就是 S 形的意思。

sigmoid 函数： $$g(z) =\frac{1}{1+e^{-z}}$$ sigmoid 函数图像：

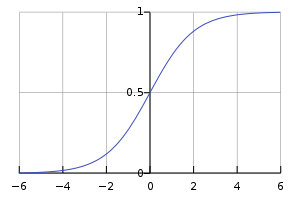
由于sigmoid函数可以将任意值映射到(0, 1)的区间内，类似求得了一个概率值。如果假设需要判断一个测试样本是否属于某一类别，设置0.5为阈值，sigmoid函数的输出如果大于0.5则认为属于该类别，小于0.5则认为不属于该类别。即可实现二分类问题。

逻辑回归的目标函数

逻辑回归和线性回归一脉相承。假设已知数据集 $\boldsymbol{X}$ ，其中有 $m$ 个 $n$ 维样本 $\boldsymbol{x}^i$ ，$i$ 代表第 $i$ 个样本。每个样本 $\boldsymbol{x}^i$ 对应着一个标签 $y^i$ ，与线性回归不同的是，这里 $y^i$ 的值是0或1，而不是任意实数。把标签值 $y^i$ 的集合（向量）记作 $\boldsymbol{Y}$ 。

逻辑回归的目标函数是一个sigmoid的函数，函数的输入就是线性回归的目标函数。线性回归的目标函数为： $$f(\boldsymbol{x}) = \boldsymbol{\theta}^\mathsf{T} \boldsymbol{x}$$ 则，逻辑回归的目标函数是： $$\sigma(\boldsymbol{x})=h_{\boldsymbol{\theta}}(\boldsymbol{x})=g(f(\boldsymbol{x}))=g(\boldsymbol{\theta}^\mathsf{T} \boldsymbol{x})=\frac{1}{1+e^{-\boldsymbol{\theta}^\mathsf{T} \boldsymbol{x}}}$$ 整个流程绘制成流程图显示如下，之所以要画这样子的流程图，是因为逻辑回归的这个流程图已经很像后续深度学习中的感知机的模样，只是激活函数使用的是sigmoid函数，这样流程图在后续的深度学习中会经常遇见：

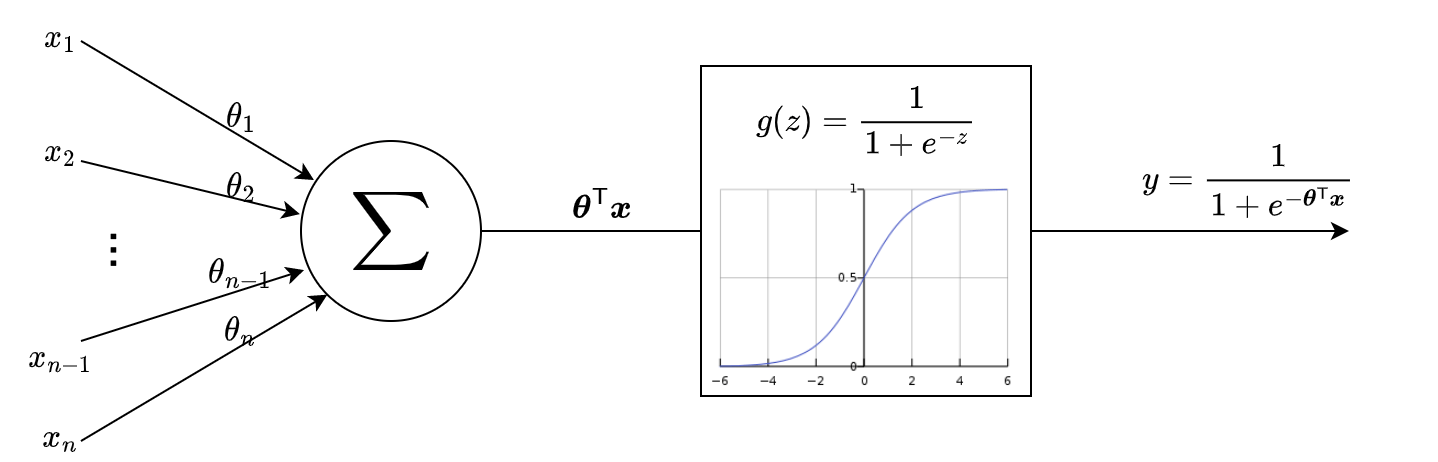
逻辑回归的损失函数

逻辑回归的损失函数是一个分段函数： $$\begin{align*} Cost(h_{\boldsymbol{\theta}}(\boldsymbol{x}), y) = \left\{ \begin{array}{lr} -log(h_{\boldsymbol{\theta}}(\boldsymbol{x})) &if \ y=1\\ -log(1-h_{\boldsymbol{\theta}}(\boldsymbol{x})) &if \ y=0 \end{array} \right. \end{align*}$$ 下图为 $-log(h_{\boldsymbol{\theta}}(\boldsymbol{x}))$ 和 $-log(1-h_{\boldsymbol{\theta}}(\boldsymbol{x}))$ 的函数图像。因为sigmod函数的输出为(0, 1)的区间，所以以下函数图像只显示(0, 1)区间的取值。可以看出当样本真实的标签为1时，预测值越接近于1则损失趋近于0，预测值越接近于0则损失趋近于无穷大；反之，如果样本真实的标签为0时，预测值越接近于1则损失趋近于无穷大，预测值越接近于0则损失趋近于0。

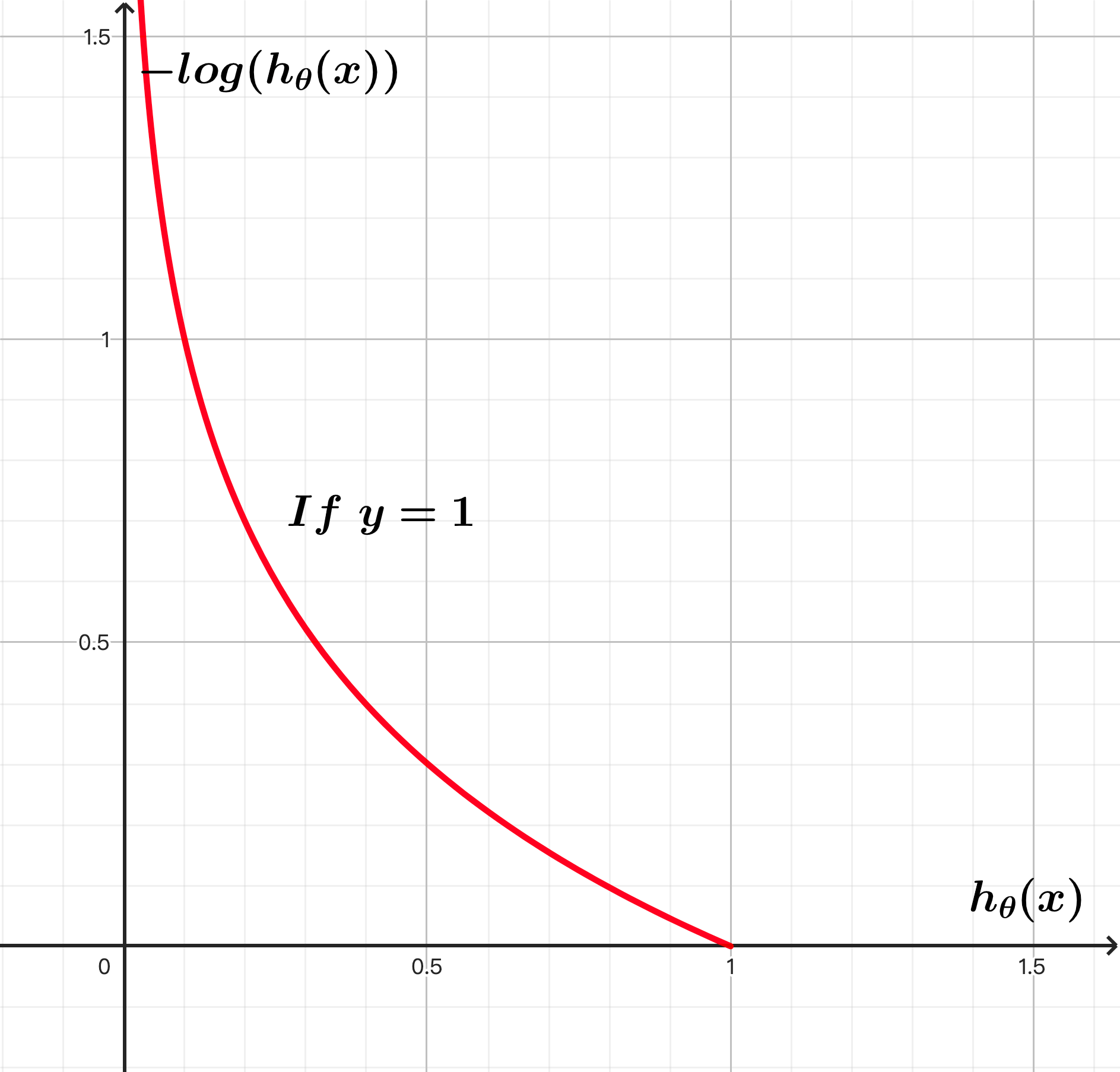
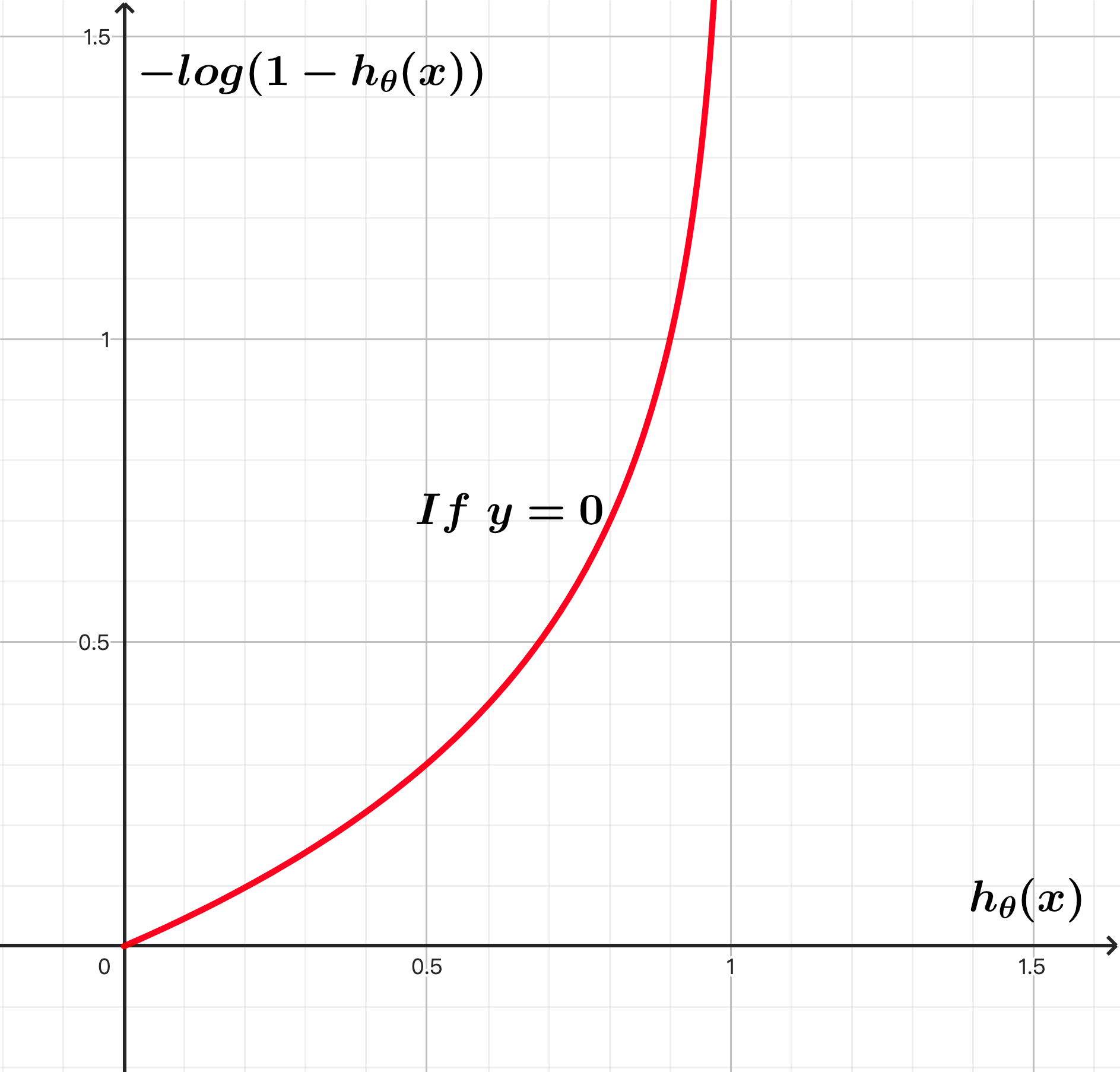
于是接下来要做的事情就是优化损失函数，找到损失函数最小时对应的参数组 $\boldsymbol{\theta}$ 。但是毕竟分段函数不利于计算，将分段函数做一下改写，这个函数就叫做负对数似然损失（Negative Log-Likelihood）函数，顾名思义这个损失函数同样可以通过极大似然估计推导而来： $$J(\boldsymbol{\theta})=-\frac{1}{m}\sum_{i=1}^{m}[y^i\cdot log(h_{\boldsymbol{\theta}}(\boldsymbol{x}^i))+(1-y^i)\cdot log(1-h_{\boldsymbol{\theta}}(\boldsymbol{x}^i))]$$ 类似线性回归，为了防止过拟合，可以加入正则化项，比如L2正则： $$J(\boldsymbol{\theta})=-\frac{1}{m}\sum_{i=1}^{m}[y^i\cdot log(h_{\boldsymbol{\theta}}(\boldsymbol{x}^i))+(1-y^i)\cdot log(1-h_{\boldsymbol{\theta}}(\boldsymbol{x}^i))]+\frac{\lambda}{2m}\sum_{j=1}^n\theta_j^2$$

梯度下降法优化逻辑回归的损失函数

先求损失函数 $J(\boldsymbol{\theta})$ 的梯度，对每一个分量 $\theta_j$ 求偏导： $$\begin{align*} \frac{\partial J(\boldsymbol{\theta})}{\partial \theta_j} &=-\frac{1}{m}\sum_{i=1}^{m}[y^i\frac{1}{h_{\boldsymbol{\theta}}(\boldsymbol{x}^i)} \frac{\partial}{\partial \theta_j}h_{\boldsymbol{\theta}}(\boldsymbol{x}^i)-(1-y^i) \frac{1}{1-h_{\boldsymbol{\theta}}(\boldsymbol{x}^i)} \frac{\partial}{\partial \theta_j}h_{\boldsymbol{\theta}}(\boldsymbol{x}^i)] \\ &=-\frac{1}{m}\sum_{i=1}^{m}[(y^i\frac{1}{g(\boldsymbol{\theta}^\mathsf{T} \boldsymbol{x}^i)}-(1-y^i) \frac{1}{1-g(\boldsymbol{\theta}^\mathsf{T} \boldsymbol{x}^i)}) \cdot \frac{\partial}{\partial \theta_j}g(\boldsymbol{\theta}^\mathsf{T} \boldsymbol{x}^i)] \\ \end{align*}$$ 其中sigmod函数 $g(z)$ 对于 $z$ 的导数为： $$\begin{align*} g'(z) &= (\frac{1}{1+e^{-z}})' = \frac{e^{-z}}{(1+e^{-z})^2} \\ &= \frac{1}{1+e^{-z}} \cdot \frac{e^{-z}}{1+e^{-z}} \\ &= \frac{1}{1+e^{-z}} \cdot (1-\frac{1}{1+e^{-z}}) \\ &= g(z) \cdot (1-g(z)) \end{align*}$$ 将sigmod函数 $g(z)$ 对于 $z$ 的导数带入前面 $J(\boldsymbol{\theta})$ 的梯度求偏导的计算过程中： $$\begin{align*} \frac{\partial J(\boldsymbol{\theta})}{\partial \theta_j} &=-\frac{1}{m}\sum_{i=1}^{m}[(y^i\frac{1}{g(\boldsymbol{\theta}^\mathsf{T} \boldsymbol{x}^i)}-(1-y^i) \frac{1}{1-g(\boldsymbol{\theta}^\mathsf{T} \boldsymbol{x}^i)}) \cdot g(\boldsymbol{\theta}^\mathsf{T} \boldsymbol{x}^i)(1-g(\boldsymbol{\theta}^\mathsf{T} \boldsymbol{x}^i)) \cdot \frac{\partial}{\partial \theta_j}\boldsymbol{\theta}^\mathsf{T} \boldsymbol{x}^i] \\ &=-\frac{1}{m}\sum_{i=1}^{m}[(y^i(1-g(\boldsymbol{\theta}^\mathsf{T} \boldsymbol{x}^i))-(1-y^i)g(\boldsymbol{\theta}^\mathsf{T} \boldsymbol{x}^i)) \cdot \boldsymbol{x}_j^i] \\ &=-\frac{1}{m}\sum_{i=1}^{m}[(y^i-g(\boldsymbol{\theta}^\mathsf{T} \boldsymbol{x}^i))\boldsymbol{x}_j^i] \\ &=\frac{1}{m}\sum_{i=1}^{m}[(h_{\boldsymbol{\theta}}(\boldsymbol{x}^i)-y^i)\boldsymbol{x}_j^i] \end{align*}$$ 对比线性回归均方误差损失函数的梯度，可以看出和逻辑回归损失函数的梯度形式上基本是完全一致的，具体见线性回归的梯度下降法。接下来利用梯度下降法对损失函数进行迭代优化即可找到最优参数 $\boldsymbol{\theta}$ : $$\theta_j := \theta_j - \alpha\frac{1}{m}\sum_{i=1}^{m}[(h_{\boldsymbol{\theta}}(\boldsymbol{x}^i)-y^i)\boldsymbol{x}_j^i]$$

通过sklearn实现逻辑回归

既然逻辑回归损失函数的梯度跟线性回归损失函数的梯度形式上完全一致，我们就不手写代码实现逻辑回归的梯度下降算法了，可以参考线性回归梯度下降算法实现。直接尝试调用sklearn中逻辑回归相关的API。

如果去翻看sklearn的官方文档，会发现linear_model中也包含了3个这样的分类器API：LogisticRegression、SGDClassifier以及RidgeClassifier，和之前线性回归的3个API非常相似。但其实它们没有对应关系。

主要实现逻辑回归的就是LogisticRegression这个接口，但是这个接口中没有包含SGD的实现。而SGDClassifier接口实现了不同损失函数下的SGD算法，其中甚至包含SVM，虽然把损失函数设置为log_loss即为SGD的逻辑回归，但该接口不是专门为逻辑回归设计的。而RidgeClassifier根本就不是逻辑回归，没有用到sigmoid函数，只是用L2正则的线性回归实现了分类的效果，具体可以参考sklearn官方文档。

本实验采用乳腺癌分类预测数据集。数据集描述：

1. 699条样本，共11列数据，第1列为id，后9列是与肿瘤相关的医学特征。
2. 最后一列表示肿瘤类型的数值：2表示良性，4表示恶性。这一列就是分类的目标。
3. 包含16个缺失值，用?标出。

既然数据有一些缺失，在逻辑回归预测之前肯定需要做一些预处理。

import numpy as np
import pandas as pd
from sklearn import linear_model
from sklearn.metrics import classification_report, roc_auc_score, roc_curve, auc
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt

column_name = ['Sample code number', 'Clump Thickness',
                   'Uniformity of Cell Size', 'Uniformity of Cell Shape', 'Marginal Adhesion',
                   'Single Epithelial Cell Size',
                   'Bare Nuclei', 'Bland Chromatin',
                   'Normal Nucleoli', 'Mitoses', 'Class']
path = "http://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data"
original_data = pd.read_csv(path, names=column_name)  # 从源地址下载数据集

def preprocess_data():
    data = original_data.replace(to_replace="?", value=np.nan)  # 将缺失值"?"替换为NaN
    data.dropna(inplace=True)  # 简单处理，把缺失值所在行丢弃
    print("Is there any null?\n", data.isnull().any())  # 检测是否还有缺失值

    x = data.iloc[:, 1:-1]  # 选择数据集第一行到倒数第二行作为样本数据
    y = data["Class"]  # 选择Class列作为标签数据
    x_train, x_test, y_train, y_test = train_test_split(x, y,
                                                        test_size=0.25,  # 设置测试集的比例占全体数据集的比例
                                                        random_state=16) # 设置随机数种子，相同的随机数种子每次都会产生完全一样的划分结果

    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)  # 对训练集数据进行标准化处理
    x_test = transfer.transform(x_test)        # 注意：这里是基于训练集标准化后的均值和方差，对测试集进行标准化
    return x_train, x_test, y_train, y_test

x_train, x_test, y_train, y_test = preprocess_data()

def LogisticRegression():
    classifier = linear_model.LogisticRegression(penalty="l2",  # 选择L2正则化
                                                 solver="sag")  # 选择sag作为梯度下降迭代算法
    classifier.fit(x_train, y_train)
    print("regr.coef_: {}".format(classifier.coef_))                           # 输出回归权重系数
    print("regr.intercept_: {}".format(classifier.intercept_))                 # 输出回归偏置

    y_predict = classifier.predict(x_test)  # 预测分类结果，给出每个样本具体的类别的判定
    y_predict_proba = classifier.predict_proba(x_test)  # 预测各分类的概率值，给出具体每个样本不同类别的概率
    y_score = y_predict_proba[:,1]  # 取第2列，也就是"恶性"（正例）的概率

    score = classifier.score(x_test, y_test)
    print("mean accuracy: {}".format(score))  # 准确率

    report = classification_report(y_test, y_predict, labels=[2, 4], target_names=["良性", "恶性"])
    print(report)  # 精确率，召回率，F1-score

    y_true = np.where(y_test > 3, 1, 0)  # roc_auc_score函数要求传入的y_true:必须为0或1，0为反例，1为正例（貌似高版本sklearn没有这个要求）
    AUC_value = roc_auc_score(y_true, y_score)  # AUC指标
    print("AUC value: {}".format(AUC_value))

    fpr, tpr, thresholds = roc_curve(y_true, y_score)  # roc_curve函数对y_true的取值是有规范要求的
    print("AUC value again: {}".format(auc(fpr, tpr)))  # 已知FPR和TPR的情况下求AUC指标
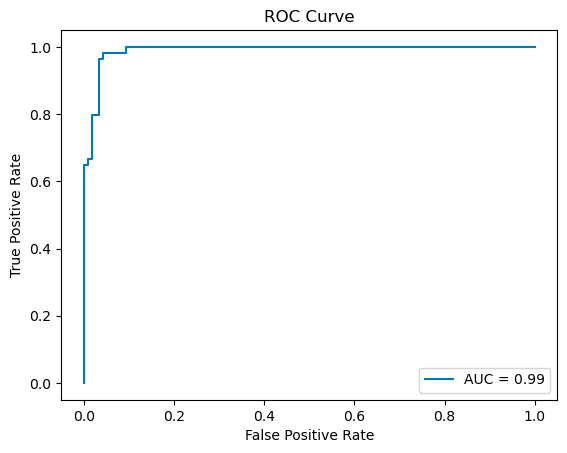
    plt.plot(fpr, tpr, label="AUC = {:.2f}".format(AUC_value))
    plt.xlabel("False Positive Rate")
    plt.ylabel("True Positive Rate")
    plt.title("ROC Curve")
    plt.legend(loc="lower right")
    plt.show()

LogisticRegression()

regr.coef_: [[1.28874969 1.07409426 1.11121314 0.61213973 0.11802989 1.34477968
  0.69445954 0.93152164 0.50223701]]
regr.intercept_: [-0.83654326]
mean accuracy: 0.9590643274853801
              precision    recall  f1-score   support

          良性       0.98      0.96      0.97       117
          恶性       0.91      0.96      0.94        54

    accuracy                           0.96       171
   macro avg       0.95      0.96      0.95       171
weighted avg       0.96      0.96      0.96       171

AUC value: 0.9893953782842672
AUC value again: 0.9893953782842672

分类问题的模型评估

以上sklearn代码包含了不少模型评估相关的内容。线性回归的模型评估相对简单，直接利用均方误差即可。但分类问题的模型评估就相对复杂。

混淆矩阵

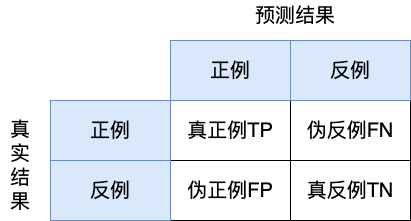
在分类任务下，预测结果(Predicted Condition)与正确标记(True Condition)之间存在四种不同的组合，构成混淆矩阵(适用于多分类)，如下所示：

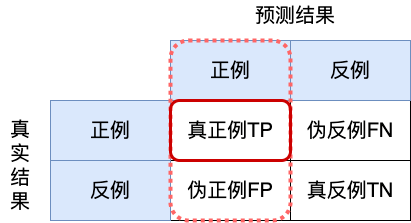
召回率(Recall)：真实为正例的样本中预测结果为正例的比例 $$Recall = \frac{TP}{TP+FN}$$

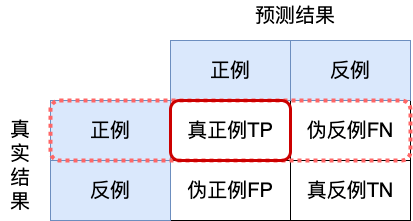
F1-score：综合考量了模型的精确率和召回率，相对比较稳健的一个评估指标 $$F1 = \frac{2TP}{2TP+FN+FP}=\frac{2 \cdot Precision \cdot Recall}{Precision+Recall}$$

ROC曲线与AUC指标

真正率（召回率）：正确的样本判断为正例的比例。所有真实类别为1的样本中，预测类别为1的比例。 $$TPR = \frac{TP}{TP+FN}$$

假正率：错误的样本判断为正例的比例。所有真实类别为0的样本中，预测类别为1的比例。 $$FPR=\frac{FP}{FP+TN}$$ 真正率和假正率是ROC曲线会用到的两个数值指标。

逻辑回归分类器的输出实际并非样本的类别标签0或1，而是(0, 1)之间的一个”概率值”，表示样本属于该类别的可能性。如果想要获得样本的标签，就需要设定一个阈值，如果概率值高于阈值则标签为1，反之则标签为0。如果调整阈值的大小，那么相应的，一部分样本的标签值可能会发生变化。

[!NOTE]

这个理解其实跟真实逻辑回归的计算不太一样。对于二分类问题，逻辑回归分类器做预测时最终会输出两个类别的概率值，哪个概率值高，样本就属于哪个类别。

假设分类器预测一个样本标签为1的概率为 $A$ ，则标签为0的概率分类器实际就是通过 $1-A$ 计算而来。然后再来判断 $A$ 和 $1-A$ 到底哪个大，然后决定最终的标签。

这样一来，对于二分类问题，阈值其实始终都是0.5，跟刚才说的调整阈值大小有点不太一样。如何理解这一点呢？实际在逻辑回归训练的过程中，可以理解为分类器将阈值设定为0.5，通过不断训练调整输出的概率值，以满足这个概率最终能被判定为相应的标签。简单说就是确定阈值，调整概率值，来达到最优化的效果。

如果我们将阈值Threshold从0开始逐步调整到1，每调整一步，就可以获得一对真正率和假正率构成的二维坐标 $(FPR,TPR)$ ，将这些坐标绘制在二维坐标系中，就会形成一条曲线。这条曲线就是ROC曲线。ROC曲线下所包含的面积即为AUC指标（Area Under the Curve of ROC），是一个数值。

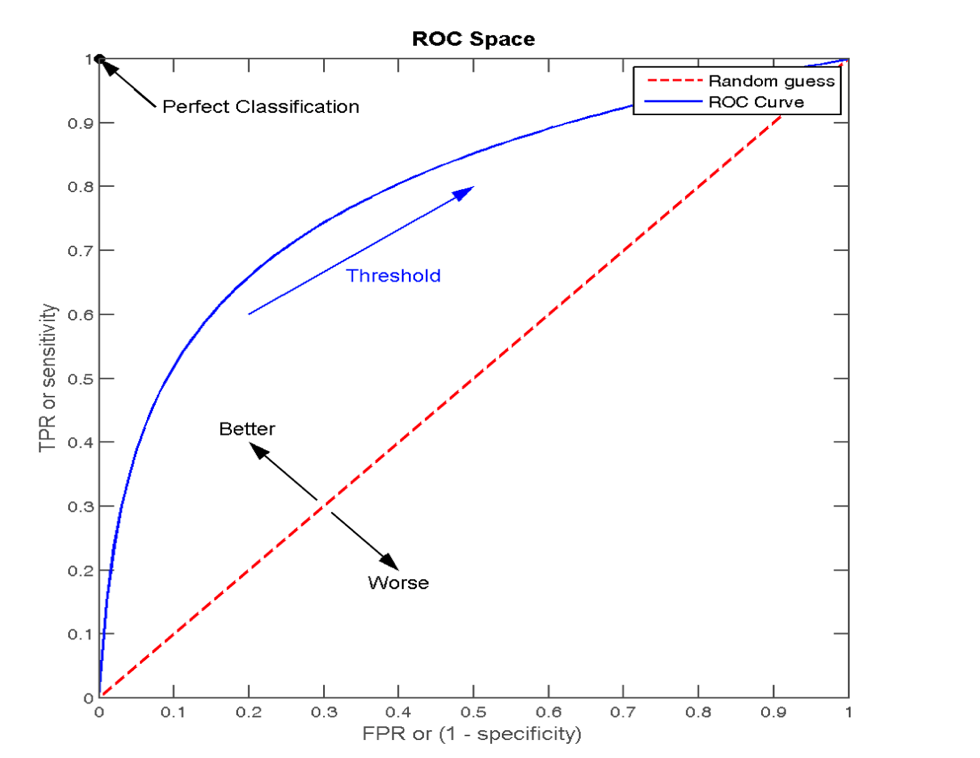
对于ROC曲线，曲线的凸起程度越高就代表着模型的性能越好，而对角线意味着一个随机瞎猜的分类器模型。从下图可以看出，三个模型 $M1$ 优于 $M2$ ，$M2$ 优于 $M3$ 。

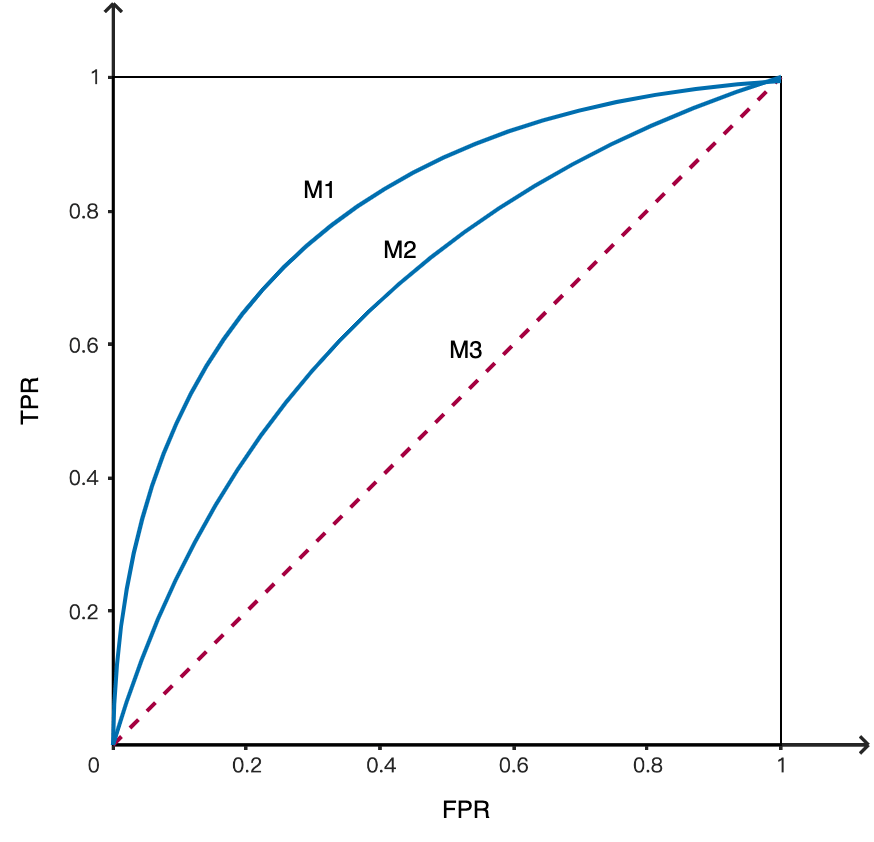
对于AUC指标，是ROC曲线下的面积，也即是被限制在1乘1方格中一部分的面积值，所以AUC指标的取值也在0到1之间。

• $AUC = 1$ ，完美的分类器，该模型至少存在一个阈值，可以将正负样本完美的划分开。
• $0.5<AUC<1$ ，优于随机猜测，数值越大，分类器越好
• $AUC = 0.5$ ，相当于随机猜测，模型没有预测价值
• $AUC<0.5$ ，比随机猜测还要差，然而若反向预测，该模型即可优于随机猜测

ROC曲线的绘制步骤：

1. 将全部样本按分类器输出的概率值降序排列。
2. 将阈值Theshold从1到0逐步减小，计算各阈值下对应的$(FPR,TPR)$数值对。实际操作中，阈值Theshold的取值可以从1开始，逐个选取按降序排列的样本概率值，直至0。
3. 将数值对绘于直角坐标系中，形成曲线。实际操作中，ROC曲线不是一个曲线，而是阶梯线，见代码示例。只有当样本量巨大时，会趋近于曲线。

用PyTorch实现逻辑回归

现在尝试用PyTorch解决乳腺癌分类预测数据集数据集的逻辑回归二分类问题。和PyTorch实现的线性回归代码做比较，可以看到，两者的差异非常小。差异只存在于：

• 模型构建的时候增加了sigmoid函数
• 损失函数采用了交叉熵损失函数BCE（Binary Cross Entropy Loss）。这里的BCE指的就是前面所说的负对数似然函数。

代码如下：

import numpy as np
import pandas as pd
import torch
import torch.nn as nn
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

column_name = ['Sample code number', 'Clump Thickness',
                   'Uniformity of Cell Size', 'Uniformity of Cell Shape', 'Marginal Adhesion',
                   'Single Epithelial Cell Size',
                   'Bare Nuclei', 'Bland Chromatin',
                   'Normal Nucleoli', 'Mitoses', 'Class']
path = "http://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data"
original_data = pd.read_csv(path, names=column_name)  # 从源地址下载数据集

def preprocess_data():
    data = original_data.replace(to_replace="?", value=np.nan)  # 将缺失值"?"替换为NaN
    data.dropna(inplace=True)  # 简单处理，把缺失值所在行丢弃
    print("Is there any null?\n", data.isnull().any())  # 检测是否还有缺失值

    x = data.iloc[:, 1:-1].to_numpy()  # 选择数据集第一行到倒数第二行作为样本数据
    y = data["Class"].apply(lambda x: 1 if x == 4 else 0).to_numpy()  # 选择Class列作为标签数据，将标签为4的转化为1，标签为2的转化为0（sklearn中不需要做这一操作）
    x_train, x_test, y_train, y_test = train_test_split(x, y,
                                                        test_size=0.25,  # 设置测试集的比例占全体数据集的比例
                                                        random_state=16) # 设置随机数种子，相同的随机数种子每次都会产生完全一样的划分结果

    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)  # 对训练集数据进行标准化处理
    x_test = transfer.transform(x_test)        # 注意：这里是基于训练集标准化后的均值和方差，对测试集进行标准化
    return x_train, x_test, y_train, y_test

x_train, x_test, y_train, y_test = preprocess_data()

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

class LogisticRegression(torch.nn.Module):
     def __init__(self, input_dim, output_dim):
         super(LogisticRegression, self).__init__()
         self.linear = torch.nn.Linear(input_dim, output_dim)

     def forward(self, x):
         outputs = torch.sigmoid(self.linear(x))  # 全连接增加sigmoid函数
         return outputs

epochs = 1000
input_dim = 9
output_dim = 1
learning_rate = 0.01

LRModel = LogisticRegression(input_dim, output_dim)
LRModel.to(device) # 如果有能用GPU计算，就把model放到GPU上去，后续就会用GPU计算
criterion = torch.nn.BCELoss()  # 二分类交叉熵损失函数（Binary Cross Entropy Loss）
optimizer = torch.optim.SGD(LRModel.parameters(), lr=learning_rate)

# ndarray转化成tensor；数据类型变为float32和模型权重参数的数据类型保持一致；如果有能用的GPU，就把数据放到GPU上去
inputs = torch.from_numpy(x_train).to(torch.float32).to(device)
# ndarray转化成tensor；形状变成n行1列的矩阵；数据类型变为float32和模型权重参数的数据类型保持一致；如果有能用的GPU，就把数据放到GPU上去  
labels = torch.from_numpy(y_train).reshape(-1, 1).to(torch.float32).to(device)

for epoch in range(epochs):
    optimizer.zero_grad() # 每一次迭代梯度要清零
    outputs = LRModel(inputs) # 前向传播
    loss = criterion(outputs, labels) # 计算损失
    loss.backward() # 反向传播
    optimizer.step() # 梯度下降迭代

    if epoch % 100 == 0:
        print("epoch {}, loss {}".format(epoch, loss.item()))

epoch 0, loss 0.6377063393592834
epoch 100, loss 0.2625509202480316
epoch 200, loss 0.1790274977684021
epoch 300, loss 0.14283452928066254
epoch 400, loss 0.12268733233213425
epoch 500, loss 0.109866663813591
epoch 600, loss 0.10099361836910248
epoch 700, loss 0.09448736160993576
epoch 800, loss 0.08951068669557571
epoch 900, loss 0.08557910472154617

softmax回归实现多分类

逻辑回归主要用来解决二分类问题，多分类问题转化为二分类再用逻辑回归显然不是一个高效的解决方案。在多分类问题中我们通常使用softmax回归。

先给出softmax函数的定义： $$\sigma(\boldsymbol{z})_k = \frac{e^{z_k}}{\sum_{l=1}^K e^{z_l}} \quad for\ k=1,\cdots,K$$ softmax函数的输入是一个向量 $\boldsymbol{z}$ ，输出也是一个向量，将输出向量的第 $k$ 个分量的值表示为 $\sigma(\boldsymbol{z})_k$ 。

softmax回归的目标函数

再次重新描述一下我们的问题：假设已知数据集 $\boldsymbol{X}$ ，其中有 $m$ 个 $n$ 维样本 $\boldsymbol{x}^i$ ，$i$ 代表第 $i$ 个样本。每个样本 $\boldsymbol{x}^i$ 对应着一个标签 $y^i$ ，与线性回归和逻辑回归都不同的是，这里 $y^i$ 的值既不是任意实数，也不仅仅只是0或1的类别标签，而是 $K$ 个类别的标签。把标签值 $y^i$ 的集合（向量）记作 $\boldsymbol{Y}$ 。

在实际操作过程中，会将 $y^i$ 表示为One-Hot编码，变成一个 $K$ 维向量 $\boldsymbol{y}^i$ ，即第一个类别表示为 $(1,0,\cdots,0)$ ， 第二类别为 $(0,1,\cdots,0)$ ，以此类推，最后一个类别为$(0,0,\cdots,1)$ 。

在具体求解时，类似逻辑回归，需要将 $f(\boldsymbol{x}) = \boldsymbol{\theta}^\mathsf{T} \boldsymbol{x}$ 带入softmax函数作为目标函数，利用极大似然估计求得损失函数，对损失函数做梯度下降优化，最终解得回归方程的权重系数 $\boldsymbol{\theta}$ 。这一套已经反复在线性回归，逻辑回归的学习中不断重复过。

与逻辑回归不同的时，此时求解的 $\boldsymbol{\theta}$ 不再是一个 $n$ 维向量，而是 $K$ 个 $n$ 维向量构成的二维矩阵 $\boldsymbol{\theta}_{n\times K}$ 。每一个样本 $\boldsymbol{x}$ 对应 $K$ 套权重系数，每一套权重系数 $\boldsymbol{\theta}_k$ 与 $\boldsymbol{x}$ 相乘后输入softmax函数得到一个相应类别的概率值。对于每个样本 $\boldsymbol{x}$ 最终会输出有 $K$ 个概率值对应 $K$ 个类别。其中，哪个类别对应的概率值大，则预测该样本属于这个类别。

所以对于样本 $\boldsymbol{x}$ ，对应第 $k$ 个类别（需要使用第 $k$ 套权重系数 $\boldsymbol{\theta}_k$ ）的目标函数为： $$h_{\boldsymbol{\theta}}(\boldsymbol{x})_k = \frac{\exp(\boldsymbol{\theta}_k^\mathsf{T} \boldsymbol{x})}{\sum_{l=1}^K \exp(\boldsymbol{\theta}_l^\mathsf{T} \boldsymbol{x})} \quad for\ k=1,\cdots,K$$ 下面还是用流程图来展示整个计算过程：

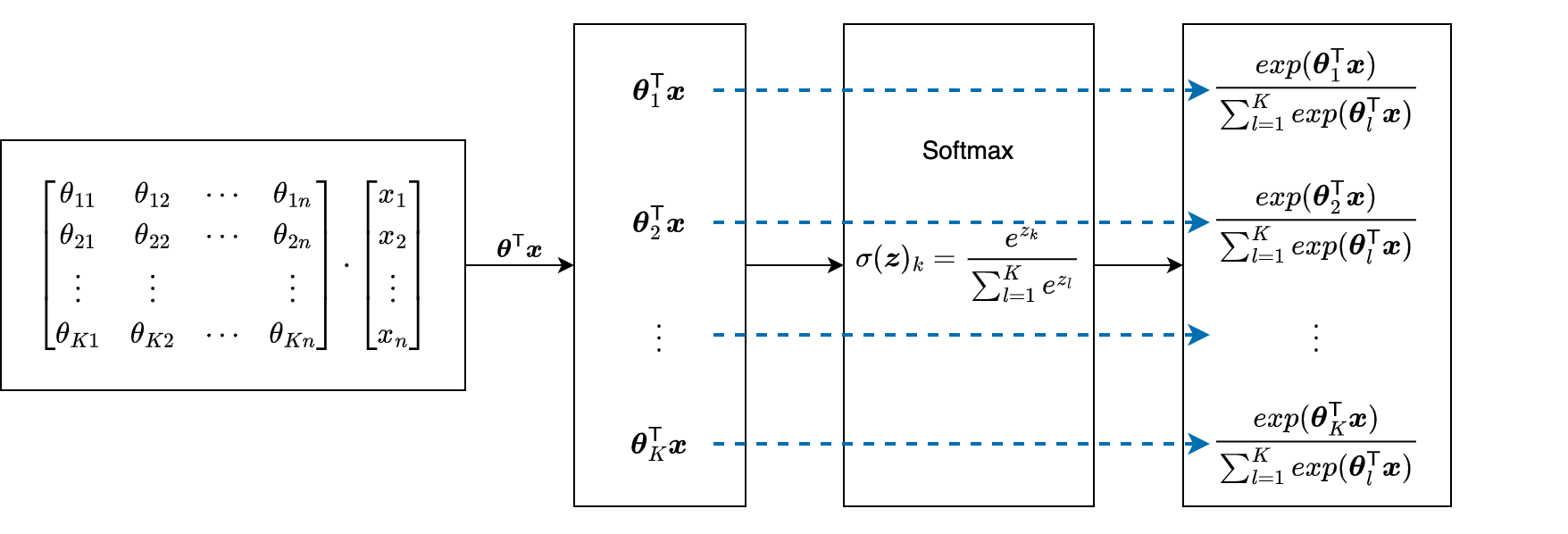
logistic回归与softmax回归的关系

现在我们再回过头来看logistic回归，其实它是softmax回归的特例，即类别数 $K=2$ ，softmax函数的输入为 $\boldsymbol{z}=(z_1,z_2)$ 。

考虑到最终我们求得的是不同类别的概率值，那么已知 $z_1$ 输出的概率为 $p$ ，那么 $z_2$ 输出的概率显然应该是 $1-p$ ，完全不用专门计算。于是 $z_2$ 具体是多少完全不重要，可以取任意值，只不过取值不同，分类器在训练的时候就会自适应这个取值，算得一套合适的 $\boldsymbol{\theta}_1$ ，最终得到一样的输出概率。那么我们令 $z_2 = 0$ ，则： $$\sigma(\boldsymbol{z})_1 = \frac{e^{z_1}}{e^{z_1}+e^{z_2}} = \frac{e^{z_1}}{e^{z_1}+e^0} = \frac{e^{z_1}}{e^{z_1}+1} = \frac{1}{1+e^{-z_1}}$$ 所以可以看出，对于二分类的softmax函数，如果令 $z_2 = 0$ ，则softmax函数转化为sigmod函数。

同时通过这个例子也可以看出，对于有 $K$ 个类别的softmax回归问题，只需要求解 $K-1$ 套 $\boldsymbol{\theta}_k$ 即可，最后一组 $\boldsymbol{\theta}_k$ 的值可以任意选取。也就是说 $K$ 分类的softmax回归问题的自由度是 $K-1$，参数矩阵 $\boldsymbol{\theta}$ 可以简化为一个 $n\times (K-1)$ 的二维矩阵。

softmax回归的损失函数

通过极大似然估计可以推导出softmax回归的负对数似然损失函数为： $$J(\boldsymbol{\theta})= -\frac{1}{m}\sum_{i=1}^m\sum_{k=1}^K(\boldsymbol{y}_k^i\cdot log\frac{\exp(\boldsymbol{\theta}_k^\mathsf{T} \boldsymbol{x}^i)}{\sum_{l=1}^K \exp(\boldsymbol{\theta}_l^\mathsf{T} \boldsymbol{x}^i)})$$ 其中，$\boldsymbol{y}^i$ 为第 $i$ 个样本的 $K$ 维标签向量，是个One-Hot编码。