决策树案例

先从一个”相亲“案例出发直观认识决策树。已知”相亲对象的条件“样本和”是否去见“的决策，可以建立一个决策树。当有新相亲对象样本来的时候根据决策树来预测”是否去见“的决策。

相亲对象的样本以及决策如下：

可以建立的一个符合以上决策的决策树如下：

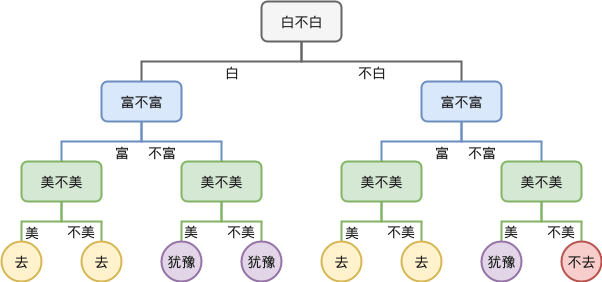
显然，如果我们先考虑富不富，再考虑白不白，则可以得到不一样的一颗决策树：

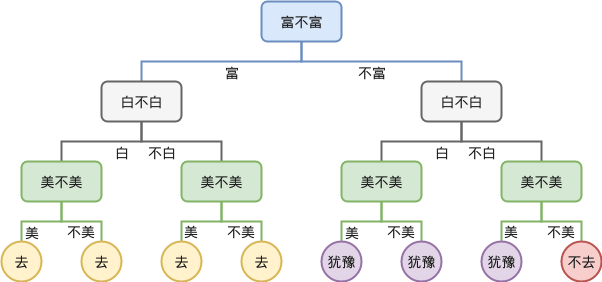
所以，可以看到，如果按照不同维度的先后顺序来建立决策树，可能会得到不同的树。

观察以上决策树可以发现其中有一些叶子节点是可以合并的，合并之后，到达某个节点时就不需要进行额外的决策，例如按照“白，富，美”顺序得到的决策树合并后如下：

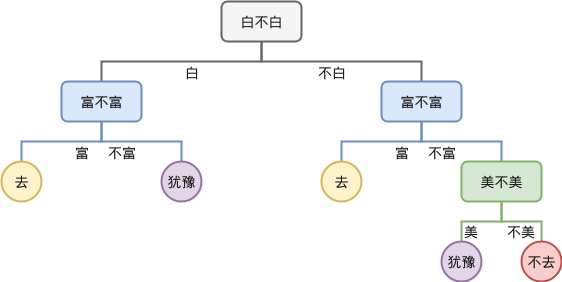
而按照“富，白，美”顺序的决策树合并后变成：

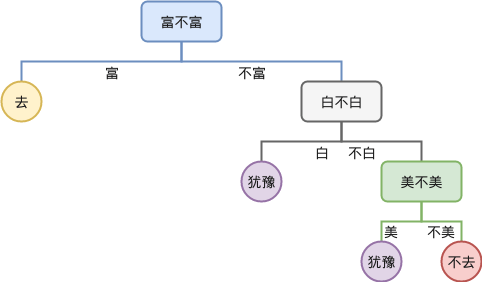
可以看到上面这棵树只有 4 个叶子节点，少于“白，富，美”顺序的决策树的 5 个节点。这就是决策树间最大的区别，不同决策树合并后得到树叶子节点的个数是不同的，后面我们会看到，叶子节点越少，往往决策树的泛化能力越高，所以可以认为训练决策树的一个目标是减少决策树的叶子节点 。

基于ID3算法的决策树构建

给出样本，建立一颗决策树并不困难。如何建立一颗好的决策树，才是需要考虑的问题。基于不同维度的先后判断顺序可以建立很多不同的树，到底其中哪棵树才是最好的那一颗？

直观上理解，如果某一个维度在做判断之后能够消除更大的不确定性，则优先判断该维度。以上例子中，如果先判断”富不富“，那么如果结果是”富“则不再需要更多的判断了，完全消除了不确定性。而如果先判断”白不白“，那么不管是”白“还是”不白“后续都后更多的判断，并未完全消除不确定性。

如何用数学语言描述”消除不确定性“？下面引入信息量和信息熵等相关的概念。

信息量

信息量在是信息“多少”的度量。例如，如下两个事件：

• 事件A：巴西队获得了世界杯冠军
• 事件B：中国对获得了世界杯冠军

仅凭直觉，事件B的信息量就比事件A的信息量要大。究其原因，是因为事件A发生的概率很大，事件B发生的概率很小。所以当越不可能的事件发生了，我们获取到的信息量就越大。越可能发生的事件发生了，我们获取到的信息量就越小。那么：

• 信息量和事件发生的概率相关，事件发生的概率越低，传递的信息量越大。
• 信息量应当是非负的，必然发生的事件的信息量为零（必然事件是必然发生的，所以没有信息量。几乎不可能事件一旦发生，具有近乎无穷大的信息量。）
• 两个事件的信息量可以相加，并且两个独立事件的联合信息量应该是他们各自信息量的和。

一个随机事件 $x$ 发生的概率为 $p(x)$ 则其信息量定义如下： $$I(x) = -\log_a p(x)$$ 如果是以2为底数，单位是bit；如果以e为底数，单位是nat；如果以10为底数，单位是det；

例如，今天下雨的概率是0.5，则包含的信息量为 $−log_2 0.5=1$ 比特；同理，下雨天飞机正常起飞的概率为0.25，则信息量为 $−log_2 0.25=2$ 比特。

信息熵

信息熵（Entropy）是接收信息量的平均值，用于确定信息的不确定程度，是随机变量的均值。信息熵越大，信息就越凌乱或传输的信息越多，熵本身的概念源于物理学中描述一个热力学系统的无序程度。信息熵的处理信息是一个让信息的熵减少的过程。

假设 $X$ 是一个离散的随机变量，且它的取值分别为 $x_1,x_2,\cdots,x_n$ ，每一种取值的概率分别是 $p(x_1),p(x_2),\cdots,p(x_n)$，那么 $X$ 的信息熵熵定义为: $$H(X) = \sum_{i=1}^n p(x_i)I(x_i) = -\sum_{i=1}^n p(x_i)\log_2p(x_i)$$ 如何理解信息熵？仍然以世界杯为例，假设世界杯32支球队获得冠军的概率完全相同，则世界杯夺冠这个事件的信息熵为: $$-\sum_{i=1}^{32} \frac{1}{32}\cdot \log_2 \frac{1}{32} = 5$$ 但实际总有一些球队获得冠军的概率更大，于是计算出来的信息熵的值肯定会小于5。也就是说，在真实世界中，世界杯夺冠这件事的信息量肯定是小于5的。越是均匀的分布，不确定性程度就越大，此时信息熵就越大。越是不均匀的分布，不确定性程度越小，此时信息熵就越小。

信息增益

对于决策树而言，当选择某个特征维度对数据集进行分类时，分类后的数据集信息熵会比分类前的小。因为我们从这个特征维度给出的样本中学习到了一些知识，这些知识帮助我们消除了一部分信息的不确定性。分类前后信息熵的差值称之为信息增益。在生成决策树的过程中，优先选择信息增益大的特征维度做划分判断，因为信息增益大的特征维度能消除更多的不确定性，也就能最终生成的决策树结构更加简单。

数学上，特征 $A$ 对于训练数据集 $D$ 的信息增益 $g(D, A)$，定义为集合 $D$ 的信息熵 $H(D)$ 与特征 $A$ 给定条件下 D 的条件熵 $H(D|A)$ 之差，即 $$g(D,A)=H(D)-H(D|A)$$

信息增益的计算方法

设训练数据集为 $D$ ，$|D|$ 表示其容量，即样本个数。设有 $K$ 个类 $C_k，k=1,2,\cdots,K$，$|C_k|$ 为属于类 $C_k$ 的样本个数，则 $\sum_k|C_k|=|D|$。设特征 $A$ 有 $n$ 个不同的取值 ${a_1,a_2,\cdots,a_n}$，根据特征 $A$ 的取值将 $D$ 划分为 $n$ 个子集 $D_1,D_2,\cdots,D_n$，$|D_i|$ 为 $D_i$ 的样本个数，则 $\sum_i|D_i|=D$ 。记子集 $D_i$ 中属于类 $C_k$ 的样本的集合为 $D_{ik}$ ，$|D_{ik}|$ 为 $D_{ik}$ 的样本个数。

则数据集 $D$ 的信息熵为： $$H(D)=-\sum_{k=1}^K\frac{|C_k|}{|D|}\log\frac{|C_k|}{|D|}$$ 特征 $A$ 对数据集 $D$ 的条件熵为： $$\begin{align*} H(D|A) &= -\sum_{i,k}p(D_k,A_i)\log p(D_k|A_i) \\ &= -\sum_{i,k}p(A_i)p(D_k|A_i)\log p(D_k|A_i) \\ &= -\sum_{i=1}^n\sum_{k=1}^K p(A_i)p(D_k|A_i)\log p(D_k|A_i) \\ &= -\sum_{i=1}^n(p(A_i)\sum_{k=1}^K p(D_k|A_i)\log p(D_k|A_i)) \\ &= -\sum_{i=1}^n(\frac{|D_i|}{|D|}\sum_{k=1}^K \frac{|D_{ik}|}{|D_i|}\log\frac{|D_{ik}|}{|D_i|}) \end{align*}$$ 以下用具体例子进行信息增益的演算，并阐释决策树生成的逻辑。

已知如下样本数据集：

计算信息增益生成决策树的过程如下：

1. 首先计算样本集合 $D$ 的信息熵： $$H(D)=-\frac{7}{10}\log_2\frac{7}{10}-\frac{3}{10}\log_2\frac{3}{10}=0.881$$

2. 计算各维度特征对于数据集合 $D$ 的信息增益，分别以 $A_1、A_2、A_3$ 为考试成绩、作业完成情况、出勤率，则计算如下： $$g(D,A_1) = H(D)-[\frac{2}{10}H(D_1)+\frac{2}{10}H(D_2)+\frac{4}{10}H(D_3)+\frac{2}{10}H(D_4)]$$ 其中 $D_1,D_2,D_3,D_4$ 分别是 $D$ 中取值为优、良、及格、不及格的样本自己。所以： $$H(D_1) = -\frac{2}{2}\log_2\frac{2}{2}=0 \\ H(D_2) = -\frac{2}{2}\log_2\frac{2}{2}=0 \\ H(D_3) = -\frac{3}{4}\log_2\frac{3}{4}-\frac{1}{4}\log_2\frac{1}{4}=0. 811 \\ H(D_2) = -\frac{2}{2}\log_2\frac{2}{2}=0 \\$$ 于是对于考试成绩这个特征维度的信息增益为： $$g(D,A_1) = H(D)-(\frac{2}{10}\times0+\frac{2}{10}\times0+\frac{4}{10}\times0.811+\frac{2}{10}\times0) = 0.539$$ 同样的方法计算 $A_2、A_3$ ，结果如下： $$g(D,A_2)=0.406 \\ g(D,A_3)=0.881$$

3. 比较各特征的信息增益，由于特征 $A_3$ (出勤率)的信息增益值最大，所以选择 $A_3$ 做为最优特征。根据出勤率把样本分为2个子集，然后把这两个子集和余下的考试成绩和作业完成情况两个属性作为输入，递归执行算法。

这样一套利用信息增益选择最优特征维度构建决策树的算法称之为ID3算法。

代码实现ID3算法

通过sklearn实现决策树

sklearn中决策树相关的实现都在sklearn.tree模块中。这里采用泰坦尼克号生存数据集来做相关的实现。

import numpy as np
import pandas as pd
from sklearn import feature_extraction, tree
from sklearn.model_selection import train_test_split

def load_and_preprocess_data():
    titanic_data = pd.read_csv("https://github.com/powerAmore/DataSciChecklist/blob/master/titanic.csv")
    x = titanic_data[["Pclass", "Age", "Sex"]]
    y = titanic_data["Survived"]
    x['Age'].fillna(x['Age'].mean(), inplace=True)  # 简单将缺失值填成平均值
    x = x.to_dict(orient="records")  # 将x转成字典类型，以便利用DictVectorizer做One-Hot编码
    dict = feature_extraction.DictVectorizer(sparse=False)  # 实例化DictVectorizer
    x = dict.fit_transform(x)  # 利用DictVectorizer做One-Hot编码
    feature_names = dict.get_feature_names()   # 返回One-Hot编码后的类别名称
    x_train, x_test, y_train, y_test = train_test_split(x, y,
                                                        test_size=0.25,  # 设置测试集的比例占全体数据集的比例
                                                        random_state=16) # 设置随机数种子，相同的随机数种子每次都会产生完全一样的划分结果
    return x_train, x_test, y_train, y_test, feature_names

x_train, x_test, y_train, y_test, feature_names = load_and_preprocess_data()
print(feature_names)  # 打印One-Hot编码后的类别名称
dc = tree.DecisionTreeClassifier(criterion="entropy", max_depth=3)  # "entropy"代表信息增益，max_depth是决策树最大深度
dc.fit(x_train, y_train)
tree.export_graphviz(dc, out_file="titanic_tree.dot", feature_names=feature_names)  # 可以用graphviz工具将dot文件转成png
print(tree.export_text(dc, feature_names=feature_names))  # 输出文字版的决策树结构
print("mean accuracy: ", dc.score(x_test, y_test))  # 准确率

['Age', 'Pclass', 'Sex=female', 'Sex=male']
|--- Sex=male <= 0.50
|   |--- Pclass <= 2.50
|   |   |--- Age <= 2.50
|   |   |   |--- class: 0
|   |   |--- Age >  2.50
|   |   |   |--- class: 1
|   |--- Pclass >  2.50
|   |   |--- Age <= 38.50
|   |   |   |--- class: 1
|   |   |--- Age >  38.50
|   |   |   |--- class: 0
|--- Sex=male >  0.50
|   |--- Pclass <= 1.50
|   |   |--- Age <= 18.00
|   |   |   |--- class: 1
|   |   |--- Age >  18.00
|   |   |   |--- class: 0
|   |--- Pclass >  1.50
|   |   |--- Age <= 13.00
|   |   |   |--- class: 1
|   |   |--- Age >  13.00
|   |   |   |--- class: 0

mean accuracy:  0.7713004484304933